模型８

円柱と円柱の交差

2011年8月6日に山口大学の吉田キャンパスで行われたオープンキャンパスで、数理科学科の説明会に訪れた高校生に、数学の話題に関連する下の写真のような紙工作を作ってもらいました。

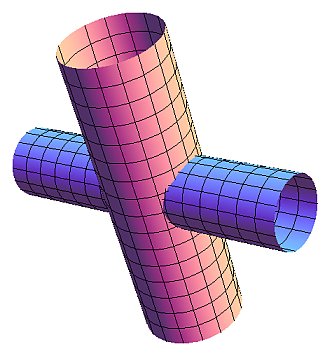
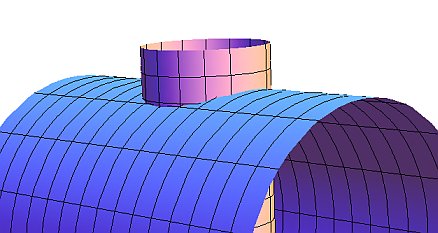
下のCGのように、半径Rの円柱に真横から半径rの円柱（R>r）を突き刺してみます。このとき突き刺された円柱の側面の展開図（突き刺された部分の穴の形）はどのようになるでしょうか？

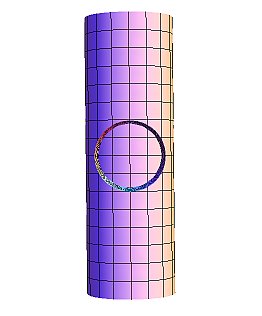
細い方の円柱の穴側から眺めると円ですが、

太い方の穴側から眺めると下のように見えます。

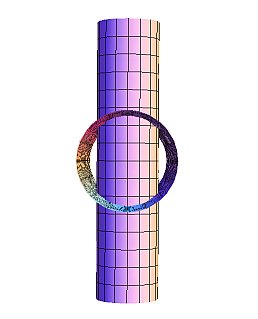
これより、大きな円柱の側面の展開図において小さい円柱で開けられた穴の形は「円」にはならないことが想像できます。
もしも二つの円柱の直径が等しい（R=r）ならば、突き刺された方の円柱（実際はどちらが突き刺された方なのか区別がつかなくなりますが）の展開図は二つに分断され、もはや穴ではなくなってしまいます。

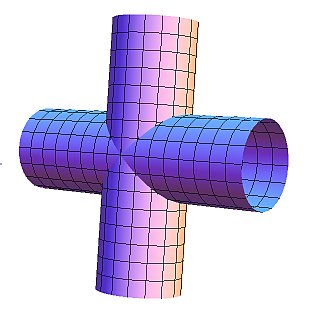
更にrを大きくすると下のようになり、展開図の切断部分は直線（厳密には上部と下部に切断する平行線）に近づくと予想できます。

Pは中心がz軸である半径Rの円柱、Qは中心がx軸である半径rの円柱とし、それらを次の方程式で表します：

これら二つの曲面の交わりは、次の関係を満たす平面上の点の集合となります：

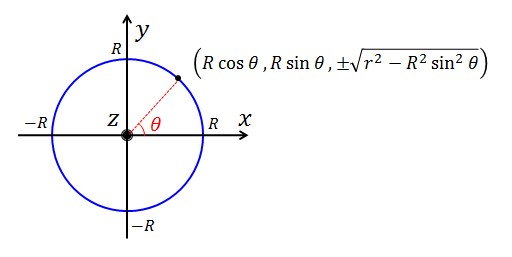
ここで、求める展開図は上の図の青線（半径Rの円柱）上の曲線となります。
縦軸をz軸、横軸（α軸）をxy平面上の青線とし座標を(R,0,0)から反時計回りに測った弧長とみなすと、α=Rθとなるので、展開図上の切り取られる曲線は次の方程式で表されることがわかります：

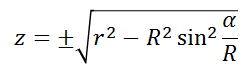
この曲線を実際に描くと次のようになります：

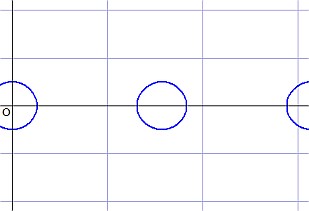（R=1, r=0.5）

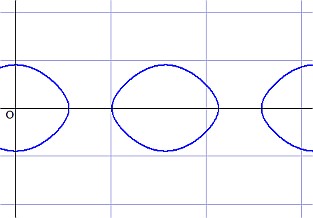（R=1, r=0.9）

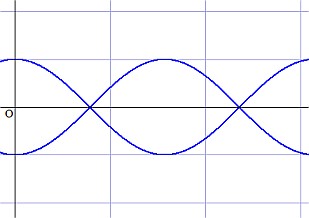（R=r=1）

（R=1, r=1.2）

製作

展開図のサンプル： sample.pdf を使い、２つの円柱の交差模型を作ってみます。

１．ダウンロードした展開図を２枚ずつ印刷してください。

２．これらを丸めて「のりしろ」の部分が重なるようにします。
（あらかじめ紙に丸みをつけ、のりよりもセロテープを使った方がきれいにできます。）

３．穴に細い方の円柱を通して完成です。
工作の精度が高ければ、つなぎ目がぴったりと合うことが確認できます。

円柱に円柱を斜めから刺した場合、円錐に刺した場合には、展開図はどのようになるでしょうか・・・・。