
工作 3
大きなものを、一定の形の小さな部品を組み合わせて作るのは工作の醍醐味です。
たとえば、レゴ・ブロックのようなおもちゃの面白さも、まさにそれに尽きると思います。
「複雑」なものを無数の「単純」なパーツを組みあわせて「近似」することは、まさに数学(この場合は解析学)の理念そのもので、たとえ「数学が嫌いと思い込んでいる人」でも、この面白さを理解できる人は「数学が好き」だと公言しても良いのではないかと思います。
今回は、ちょっとしたきっかけで製作を思い立った下のような「球体」の模型を紹介します。

山口大学理学部主催で毎年行われている理学部サイエンスワールドの出展ネタとして、昨年は同じ太さの角材(断面が1辺約1cmの正方形)を集めて下のような球体を製作しました。

この立体は、長さの異なる216本の角材を並べて球を近似したもので、工程はまさに積分の概念そのものです。
木材の切断に果てしなく時間を費やしたものの、製作過程は楽しく完成品もまずまず満足ゆくものだったのですが、次のような点に不満が残りました。
製作費: 角材の単価はたいしたものではありませんが、このように大量に使うと無視できない金額になってきます。ちなみに、この球体の製作には角材の費用だけで8000円くらいかかっています。
材料の精度: 一見均等に見える角材の太さも、実はコンマ数ミリ程度の誤差があります。これは無視できない量で、実は完成品を近くで見ると角材同士の間に隙間が見えます。
加工精度: 写真の球を地球に見たて、北極あたりをよく見ると、赤道付近と比べて角材の長さがほとんど同じであることがわかります。実際、北極から南極を貫く付近の角材の長さは0.1ミリ単位の差しかないのですが、薄いものでも0.3ミリ以上の厚さがあるノコギリを使ってこの精度を実現するのは非常に困難です。
このように、単純なパーツを組み合わせて大きく精巧な立体を実際に製作する場合、実はパーツの「精度」と「単価」が最も重要な問題になります。
そこで、今回パーツとして使用したのが「BB弾」です。これはエアガンに使用する弾丸なのですが、飛距離や命中精度を高めるために精巧な部品で作られた最近のエアガンに対応するため、この弾丸の方も大変高い精度で加工されています。また、屋外で大量に使い捨てられるため単価も安く、どこでも簡単に手にいれることもでき、今回のような用途にはうってつけの素材です。
材料さえ決まれば、後は「設計」と「加工」です。
この模型も他と同様、芸術作品ではなく、あくまでも「数学の教材」なので、設計にあたっては数学的背景をそれなりに説明しておく必要があります。
1.設計
同じ大きさの球を積み重ねてゆき、最も安定した高密度の状態が六方最密充填構造です。数学では球充填という有名な問題で、古くから研究されています。
今回の球の模型のイメージは、上記の充填構造(正規充填)を持ったBB弾の塊があり、そこから、できるだけ球に近い形が残るように余分なBB弾を取り除いてゆくといったものです。塊から取り除く部品をいくらでも細かくできれば、例えば木片から削り出すような場合、少なくとも見かけ上は完全な球を作りだすことができます。しかし、今回のように取り除く部品の大きさが決まっている場合、「取り除く場合と取り除かない場合のどちらが球に近くなるか?」を判定しなければなりません。今回採用した方法を数学らしく説明をすると次の通りです。
・BB弾1個の直径を1単位とし、正規充填されたBB弾の塊の中に半径10の球を考える。
・それぞれのBB弾の中心の座標を考え、それが上記の球の内側にあればそのBB弾は残し、外側にあれば取り除く。具体的には、中心の座標をが(xk,yk,zk)であるBB弾 「Bk」に対して次のような判定を行います。
![]()
![]()
実際には、BB弾の塊から取り除く作業は現実的ではないので、上の判定条件を満たすようにBB弾を積み上げて球を構成してゆきます。
ちなみに、1段目は下の写真のようになります。

1段目のBB弾の中心の座標は
![]()
となることは明らかですが、2段目以降のz座標は少し考える必要があります。
実際、2段目を積み重ねると下の写真のようになります。

(2段目は黄色で、黒の部分には本来BB弾はありません。積み重ねる都合上置いたものです。)
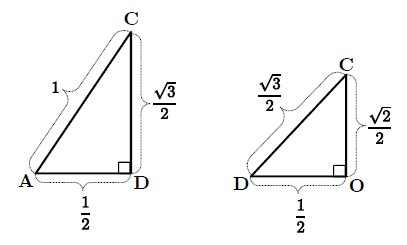
2段目の (x, y) 座標が整数の格子点となることは明らかですが、以下の図に注意してz座標を計算すると、2段目のBB弾の中心の座標は次のようになることがわかります。
![]()

このようにして、一般にk段目のBB弾の中心の座標は次のようになることがわかります。

このようにして、k段目にはどのようにBB段を配置すればよいかが計算できます。ちなみに、5段目の配置は次のようになります。

2.充填密度と円周率
直径の1(半径1/2)の円と一辺の長さが1の正方形の面積比は次のようになります。
![]()
よって、平面上に、整数の格子点を中心とした半径1/2の円を敷き詰めてゆくと、平面の中で円の面積の占める割合の平均(ここでは「密度」と呼ぶことにする)は「π/4」となります。
ところで、半径10の円の面積は
![]()
となります。この形を上の絵のように半径1/2の円で再現しようとすると当然隙間ができますが、それは上で紹介した意味での「密度」が1より小さいためです。よって、半径1/2の円で再現した半径10の円の面積は理論的には次のようになります。
![]()
ところで、今回製作した模型の1段目では、半径10の円を半径1/2のBB弾316個で再現しています。これを「半径10の円を半径1/2の円316個で再現した」とみなすと、その面積は次のようになります。
![]()
このことから、既に計算した理論値より、π に関する次の近似式が得られます。
![]()
この考え方を、次は正規充填で近似された球で考えてみます。
先ほど、平面に敷き詰めた円の平均密度を計算しましたが、同様にして、空間に正規充填された球の平均密度を計算することができ、その値は次のようになります。
![]()
また、半径10の球の体積は
![]()
となるので、これを半径1/2の球で再現したとき、その体積は
![]()
となります。ところで今回の球の製作に使用したBB弾の総数は5866個なので、こららの体積の合計は
![]()
となります。よって理論値から求められる π の近似値は次のようになります。
![]()
3.表面に現れる模様と多面体
次の2枚の画像を見ると、この球が「6枚の正方形」と「8枚の正六角形」でできていることがわかります。
これは、半正多面体の一種である「切頂八面体」と呼ばれる多面体で、立方体の8つの頂点を切断面が正六角形になるように切り落としたものです。


4.おまけ
「エポック社」が作っている「アクアビーズ」という子供向けのおもちゃがあります。
これは、直径5mmの水溶性のビーズ同士を水でくっつけていろいろな形を作ることができるというものです。
単価(1個1円弱)や精度の問題で今回はこれを使いませんでしたが、小さいサイズのものを試しに作ってみるには悪くないのではないかと思います。ただし、少し大きなものを作ろうとすると驚くほどコストがかさんでゆくので注意して下さい。