
模型9
線織面(鞍型)
何年も前から作ろう作ろうと思いながら手を付けていなかった鞍型の模型をようやく作りました。

これは、(x,y,z)空間上の曲面 z=f(x,y) 上の点(x_0,y_0,f(x_0,y_0))で、偏微分係数が0:
![]()
でありながら、その点では極値をとらない典型的な例です。
「模型2」では、半径1の円柱の側面に描いた曲線C:
![]()
上の2点
![]()
結ぶ直線の軌跡が描く曲面を考えました。

しかし、C上の2点の選び方を変えると描かれる曲面も変わってきます。
C上の点Pと次の点Rを結ぶ直線を考えてみます:
![]()
これらの点をz軸方向から眺めると次のようになります:
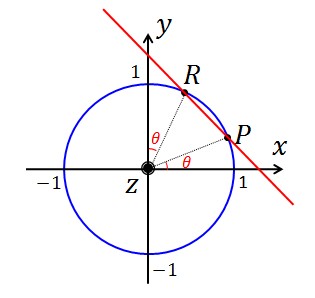
2点PRを通る直線の方程式は、kをパラメータとして
![]()
と表されますが、
![]()
より、この直線の描く軌跡は次の関数で表される(x,y,z)空間上の曲面であることがわかります。
![]()
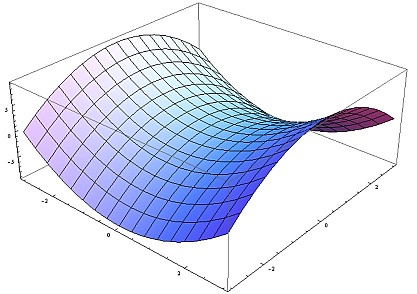 z=x^2-y^2
z=x^2-y^2
この曲面は「双曲放物面」とよばれる2次曲面の一種で、直線の運動によって描かれる「線織面」(せんしきめん: ruled surface)とよばれる曲面の一種です。
製作
製作は、基本的に「模型2」の場合と同様ですが、今回は円筒として、直径100mm、厚さ2mmのアクリルパイプを使い、側面から斜めに穴を空けなければならないので、少しだけ注意して加工する必要があります。
製作途中の写真は撮っていなかったので、完成写真だけ紹介します。