模型１８
トーラス結び目のスライス
ドーナツをねじった「結び目」のあるトーラスのモデルを製作しました。数式では次のように表すことができます。
・・・（１）
ここで、Rは２より大きい定数です。この立体は、位相幾何学の分野では「（２，５）型トーラス結び目」とよばれ、下の写真のように、穴のあいたリングの周りを、穴を左（または右）に見て２周しながら、リングに５周巻きつく紐の形状に相当します。
以前、下の写真左のような、立体を xy 平面で切断した断面図を積み重ねたモデルを製作しましたが、今回は写真右のように xz 平面と平行な平面で切断した断面図を並べたモデルを製作します。
まず、平面 y=d における切断面を数式で表してみます。
（１）の2式に y=d を代入して sin t について解くと
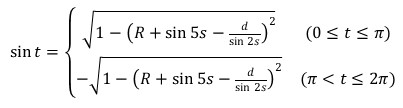・・・（２）
これを（１）の１式・３式に代入すると次が得られます。
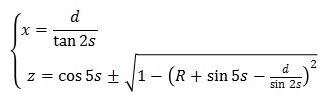・・・（３）
xz 平面上で上記の (x, z) をパラメータ s を 0 から 2πまで変化させれば断面図の曲線が描かれます。
型紙製作には（３）で十分ですが、ここから更に s を消去してみます。（３）の１式を s について解くと次のようになります。
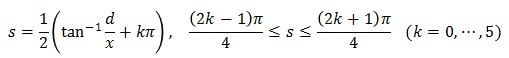
これを（３）の２式に s に代入すると z を x の式で表すことができます。このグラフを、例えば R=3 とし、d = 0.3, d=1.5 の場合に描くと次のような曲線になります。
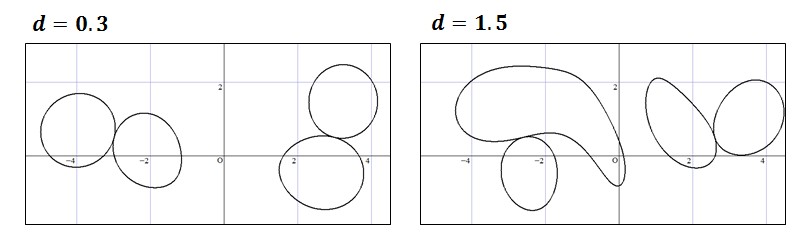
d を少しずつ変化したときに描かれるこのような断面図を並べて作ったのが今回のモデルです。
製作過程
（１）パーツの製作
断面図の部品： 横幅120mmの４７枚のケント紙で作りました。
隙間の部品： 断面図の部品の隙間を埋める厚紙です。上の４７枚の部品の隙間に等間隔に挟んでゆき、最終的に厚さが120mmになるように部品の厚さを調整しています。
パーツを並べる台： 木材を切ってニスを塗ったものです。
（２）部品を並べる
型紙ダウンロード（幅50mmバージョン）
※この型紙は、１００円ショップに売っているコレクションケース用に設計したものです。
