工作 ４

2008年11月に行われた理学部サイエンスワールドの出展ネタとして、下のようなボールを製作しました。

これは、球の体積を、無数の直方体で近似するという「積分」のイメージをモデル化したものです。

積分の話

積分とは何かということを、円の面積の計算を例として簡単に解説しておきます。

円の面積を求める方法はいろいろありますが、その中の一つとして次のような考え方があります。

（x,y）平面上の原点を中心とする半径１の円は、次の方程式で与えられます。

y≧0 の場合、この円周の y座標を xの関数として表すと次のようになります。

x≧0 の場合にこの関数のグラフを描くと、そのグラフとx軸、y軸に囲まれた部分が、半径１の円の4分の1の面積、すなわち「π/4」になることがわかります。すなわち、円の面積を求めるということは、その部分の面積を求めることに相当します。

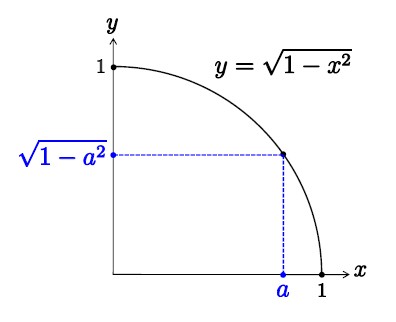
では、実際にその部分の面積を「計算することを試みて」みましょう。

図のような曲線で囲まれた部分の面積を求めることは難しいので、とりあえず「求めたい面積に近く実際に求めることのできる面積」を計算してみることにします。「実際に計算することができる面積」として、ここでは長方形の面積を考えます。

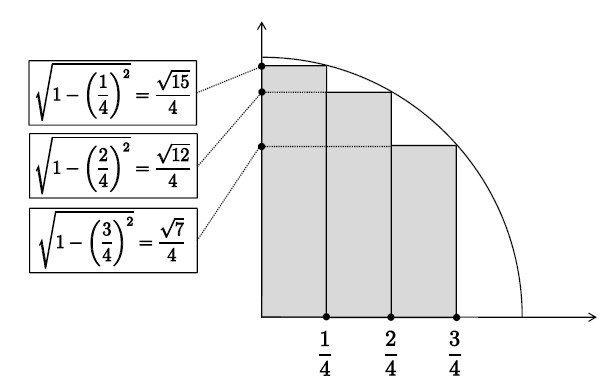
図のように、求めたい部分の面積の内側に３（＝４−１）個の長方形を考えると、その面積は次のように計算することができます。

ちなみに、これを４倍すると 0.6239…×4 = 2.4957… となります。

これが半径１の円の面積：π = 3.1415 に近いかどうかは微妙な気がするかも知れませんが、求めたい部分の内側に考える長方形の数を増やすと、 真の円の面積により近い値が計算できるのではないかと期待できます。

そこで、上の式を敢えて次のように表現しておきます。

すると、上の考察を一般化し、横の長さが一定の「N-1個の長方形」の面積 S_N で4分の1の円を近似した時、その値は次のように与えられることが分かります。

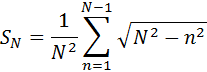
例えば、99個の長方形で近似した場合、N = 100 となるのでS₁₀₀は次のように計算されます。

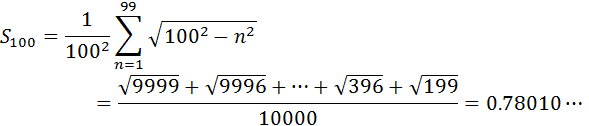
このとき、4×S₁₀₀ = 3.1204… となり、4×S₄ = 2.4957… よりも π = 3.1415 に近づいたことはわかります。

参考までに、4×S₁₀₀₀₀ = 3.14139… となり、Nの数を増やすほど、4S_N は π の値に近づくことがわかります。

この考え方を応用し、求めることが難しい曲面に囲まれた「球」の体積を、その内部に「実際に体積を計算することが可能」な直方体を考え、その体積の和によって近似してみることにします。

今回製作したのは、上記の積分のアイディアを角材を使った模型で表現したもので、実際は２１６個の長方形で球を近似しています。 ちなみに、半径１の球を上記ように近似した場合、２１６個の長方形の体積の和は「3.502…」となります。これが近似したい半径１の球の体積：4.18879…に近いかどうかは微妙な気がするかも知れませんが、少なくとも完成した模型は結構球体に近いように見えます。

模型の製作

ＢＢ弾で作る球と比べ、この球体の模型の設計は極めて単純です。大変なのは木を切る作業で、特にコンマ１ミリの誤差で角材を切断する作業にかなり神経を使います。（実際にはそのような精度で加工できているわけではありませんが。）

加工した角材の山

並べたところ

積み上げたところ（設計図片手に部品の長さを測りながら積んでゆかなければなりません）

完成品

材料費と気力があれば、より多くのパーツを使ったものを作りたいと思っています。

Back