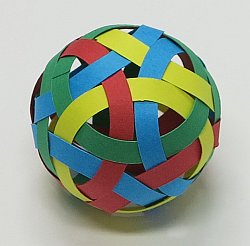
2012年 数楽工作倶楽部 第5回製作物
今回は厚紙の帯で編む多面体の製作行程を紹介します。
クラフトバンドで編む多面体は以前に紹介しましたが、今回のモデルは少し難易度が上がります。
このモデルのベースとなったのは、以前に紹介した菱形六十面体で、位相的には全く同一のものと考えられます。です「球」のように編むには多少工夫が必要です。
ちなみに、上のモデルを何の工夫もせずに「円環」で編むと、下のようなものが出来上がります。このリング同士の交わる箇所を頂点、それらを結ぶリング上に辺を考えると、このモデルは「斜方二十・十二面体」と考えることができるでしょう。

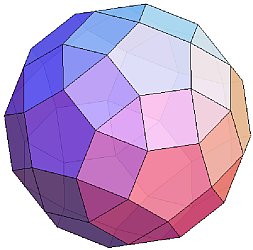
このモデルはお世辞にも球とは言い難いですが、その原因は単なる円環で作ったリングで編んだことにあります。
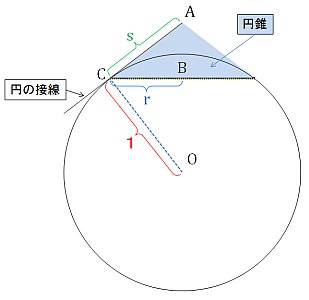
よって、もしこのリングを「球の面に沿うような角度」がついたもの、すなわち、下のような「球に接する円錐の一部」に置き換えてやると。より球に近い形になるのではないかと期待できます。

ここで、円錐の底面を、下図のように斜方二十・十二面体中の正十角形の外接円と考えることにします。

斜方二十・十二面体の一辺の長さと外接球の半径の比は
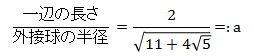
よって、この斜方二十・十二面体の外接球の半径を1とすると、黄色の点線が表す一辺が a のせい十角形の半径 r は次のようになります。
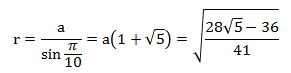
このとき、円錐の稜線の長さを s とすると、s の値は次のように表すことができます。
![]()
従って、この円錐の展開図の扇形の中心角θは次のようになります:
![]()
これをもとにリングの型紙を作成します。
製作工程
今回は、3本×4色、合計12本のリングを使います。12本は正十二面体の面の数、4色は正十二面体の各面を塗り分ける色の最少の数に由来しするものです。



今回は、直径90mm・太さ8mmの円環を使いましたが、初めて作る場合には、もっと大きなリングの方が作りやすいと思います。(円をきれいに早く切り抜くには、円切りカッターが便利です。)
切り取った円環を、先ほど計算した中心角が213度になるように切り取ります。("のりしろ"の部分を残しておくこと!)
あとは、切り抜いた部品を下のように組んでゆくだけです。ボールなどの上で組むと作業が容易になると思います。



(画像の一部はクリックすると拡大します。)
あとは、リングが交互になるように適当に組んでゆくと完成します。
正十二面体の塗り分けで、隣接する面と色が異なるのは、同じ色のリングが交差しないことに対応します。(実は上のモデルでは組み上げに失敗しています!きちんと組むと、最上段のモデルのように4色で同じ色が重ならないようにすることができます。)