
2013年度 数楽工作倶楽部 第5回製作物
3次元のハート形

x と y の方程式 F(x,y)=0 の解 (x,y) を (x,y) 平面上にプロットしてゆくと、次のようないろいろな形のグラフが現れます:


一般に、x, y の次数を大きくすると、方程式の解である点は、(x, y) 平面により複雑な曲前を描きます。
上のグラフの上段は1または2次方程式、下段は左から2、3、4次方程式です。
6次方程式では、解の点が下のような「ハート形」になるようなものを考えることもできます。
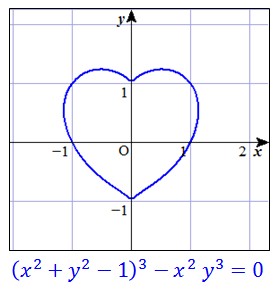
今回は、上のハート形を3次元に拡張した次のような方程式の解が(x,y,z) 空間上に描く立体を紙工作で再現してみました。
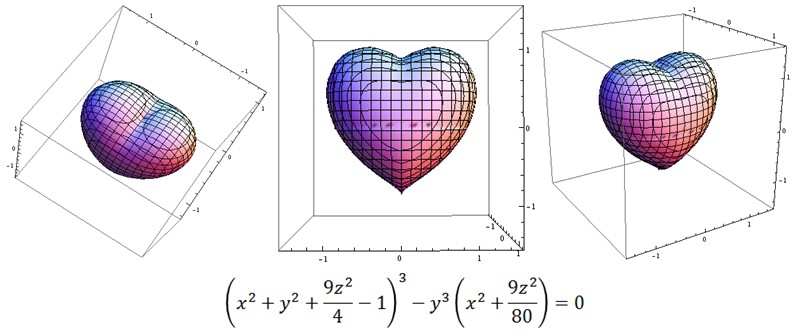
ここで、上の方程式に z=0 を代入した式、すなわち (x, y) 平面での切断面は、(x, y) 平面上のハート形の方程式になります。
ちなみに、上の式中の 「4, 9」 は、単に z 方向の形状を決めるパラメータです。
以前に同じ立体を、xy平面に平行な平面でスライスした等高線の曲線を重ねて下のように 再現したことがありますが、今回は yz平面に平行な平面で切断した曲線を並べることによって再現します。(ただし、今回は z が正の部分だけを再現しています。)

設計自体は特に難しいところはありません。上の方程式に x=d を代入し、d を変化させた (y, x) 平面上の曲線群を切り出すだけです。
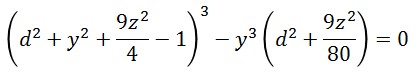
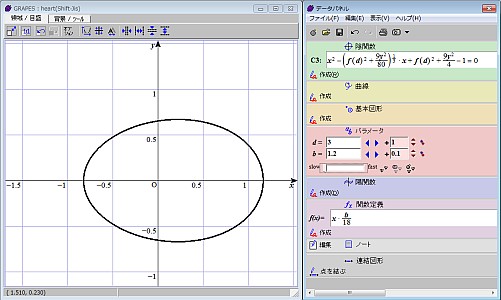
今回の模型の型紙製作には、陰関数の曲線を描かせるために「Grapes」を使いました。
製作風景(画像をクリックすると拡大します)
1.部品の切り抜き
2.部品を並べる
部品と部品の隙間に厚めの両面テープを貼ってゆきます。
(ずれると修正ができないので慎重に!)
3.完成
