
2014年度 数楽工作倶楽部 第3回製作物
格子で作る曲面(2)
トーラス

第2回に引き続き、立体(曲面)を格子状の切断面から再現してみます。今回は、以前に扱ったトーラス(ドーナツ型)を作ってみました。
今回制作するトーラスは、(x, y, z) 空間上の次の方程式を満たす点の集合として与えられます:
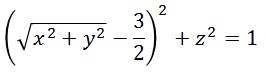
「方程式を満たす点の集合」とは、次のように考えることができます。
上の方程式を z について解くことにより、方程式が与える空間中の z 座標は、次のような x と y の関数として与えることができます。
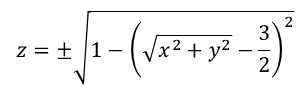
例えば、x=y=1 の場合、z 座標は次のようになります。

従って、方程式を満たす点として (1, 1, 0.9963...),(1, 1, -0.9963...) が選ばれます。
このような操作を繰り返すことによって、空間中に選ばれた点を集めると下のような曲面が現れます。
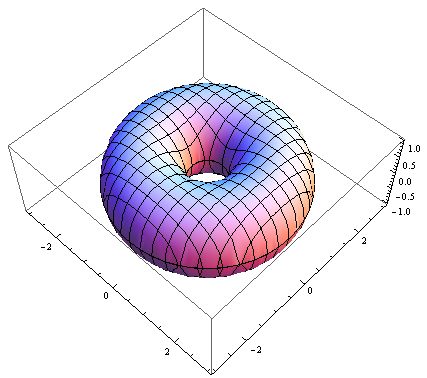
ちなみに、z が実数(ルートの中身が非負)でなければ実際に点を打つことができません。
そのための (x, y) に対する条件は

なので、z は次のような (x, y) 平面上の円環領域のみで値(実数値)をとります。
(真上から見るとドーナツ形となるのはそのためです。)
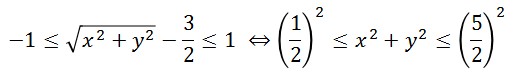
この立体を平面 x = a で切断すると切断面を囲む曲線は次のようになります。
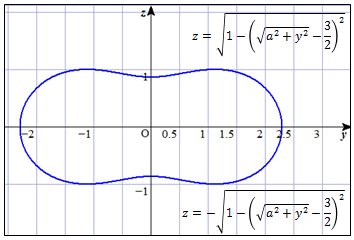
(a = 0 の場合)
a を少しずつ変化させ、現れる切断面を並べたものが昨年度に製作したものでした。

同様に、平面 x = a と垂直な平面 y = b で切断した面を考え、それぞれを垂直に組み合わせたものが、今回の製作物です。
製作
型紙を適当な厚紙2枚に印刷します。[型紙ダウンロード]
作り方は、前回の2次元正規分布のモデルと同じです。ただし、切り込みの幅が広すぎると、すぐに崩れてしまうかも知れません。